Привет всем!
Давненько не было увлекательных постов на тему программирования, математики и вычислительных экспериментов. Сегодня как раз будет такой. Несколько дней назад в ютубных рекомендациях (ох уж эти алгоритмы) промелькнул шортс, где молодой человек рассказал про так называемые «совершенные» числа. Так вот, оказывается, совершенное число — это такое число, сумма собственных делителей которого равна этому числу. Например, число 6 : считаем 1 + 2 + 3= 6. Далее идёт число 28. Его собственные делители 1, 2, 4, 7, 14, и их сумма 28. Далее эти числа дико возрастают: 120, 496, 8128…. Потом этот шортс с числами куда-то плавно уехал, а на его место подъехал какой-то садовник, который зачем-то жёстко наказал высокомерную певицу за наглость и унижение людей, а я так и остался в оцепенении от этих чисел. Шли серые рабочие будни, тренировки мелькали одна за другой, а я всё думал об этих совершенных числах: сколько же их всего в природе и как их найти? Конечно, есть довольно подробная статья в Википедии. Изучив её, немного прояснилось: оказывается всего их на данный момент известно ровно 51 штука. Первые девять были найдены до конца 19-го века. Дальше вы понимаете — лампочка Ильича и пошло-поехало. Но всё же, это всё было очень таинственно и притягивало как магнитом.
Я сам не заметил, как начал писать код. Было интересно реализовать два момента:
1. Хотелось бы загрузить все 8 ядер (12 потоков) моей ЭВМ по самые помидоры.
2. Хотелось бы реализовать прогноз времени финиша расчёта. Узнать, сколько секунд, часов, дней и лет понадобится для поиска собственных делителей хотя бы тех совершенных чисел, которые были найдены до начала 20-го века.
Прошло около недели беспокойных вечеров, помощь друга и вот скриншот софтины:
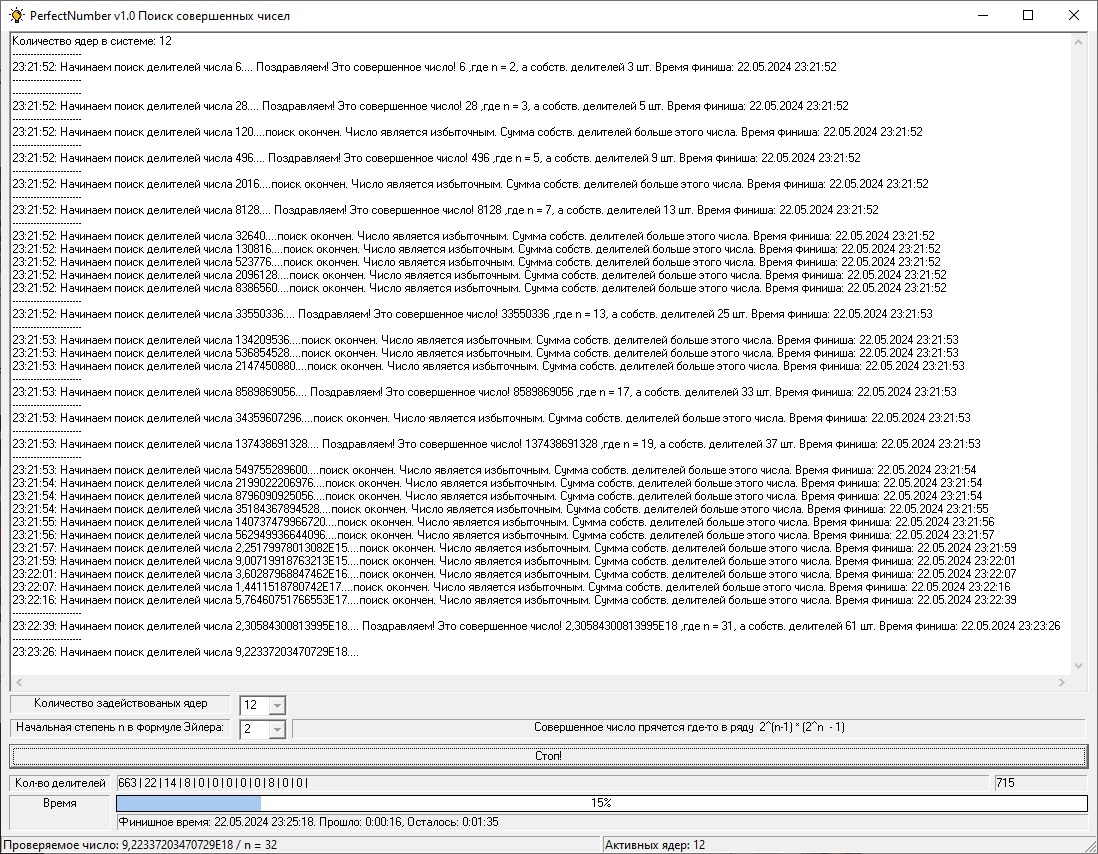
Как видно на этой картинке, было реализовано почти всё, что задумано. Чётные совершенные числа принадлежат степенному ряду Эйлера, формула которого приведена. То есть, нет смысла перебирать все числа в мире, достаточно прожарить всей мощью процессоров этот ряд и выявить в нём подходящие, то есть совершенные числа. Цикл поиска делителей любого числа является линейным алгоритмом, а значит, его можно раздробить на любое количество отрезков и перемалывать по-отдельности. Ну, как вы догадались, количество этих отрезков – это количество ядер на вашем железе. Затем делители осталось просуммировать и сравнить с претендентом на «совершенность». Если они равны, то и число совершенное! Если сумма больше, то такое число называют избыточным. Если же меньше – недостаточным. При этом сразу видно, что делители числа расположены неравномерно по числовой оси. Внизу их всегда больше. Алгоритм поиска делителей реализован максимально быстрый – пробег в цикле идёт не до самого числа, и даже не до половины, а до корня квадратного этого числа! При нахождении одного делителя – очевидно сразу известно и второе — парное ему — через лишь одну операцию деления. Реализована возможность загрузить любое количество имеющихся на вашем железе ядер. Скорость вычисления от этого меняется строго пропорционально.
Итого, что же мы имеем по скорости вычислений ? А в сухом остатке имеем следующее: первые восемь совершенных чисел моя ЭВМ находит примерно за полторы минуты ! Кстати, восьмое число по счастью имеет порядок n=31, а само число, стало быть 2^30 * 2^31, т.е. 2^61, что укладывается в разрядность 64-х битной ЭВМ. А вот дальше уже интересно. Следующее, девятое по счёту, известное науке число имеет порядок 2^121. И если, даже зная об этом числе, запустить его на проверку «совершенности», то ЭВМ показывает финишное время – март 2026-го года. Ну, то есть, нужно немного потерпеть. Далее в процессе вычислений, как водится, время финиша будет постепенно уточнятся, но прогноз всё равно неутешительный. Когда на работе запустили эту проверку на 20-ядерном Core i7 12700K, так над прогнозом ржали всем коллективом. Но дело даже не в этом. Ошибка здесь в том, что при максимально быстрых целочисленных операциях поиска делителя, само число не может быть больше 2^64. На лучшем во Вселенной языке программирования Си этот тип называется unsigned long long или же __int64. В случае же этого девятого совершенного числа, оно будет иметь разрядность 2^121, что сильно вываливается за границы возможного диапазона. Так как 121-разрядных ЭВМ нам пока не подвезли, то остаётся вариант расчётов с плавающей точкой. Срочно перегнал расчёты в тип double, что раздвинуло рамки поисков до 308-й степени двойки. Можно скачать первую версию и развлечься. Кстати, обычно математики ограничиваются поиском простых чисел Мерсенна из ряда 2^n — 1, из которых уже вытекают совершенные числа. На сегодня 51-е число Мерсенна равно 2^82589933 — 1. Найдено оно было в 2018-м году, и если записать это число на бумаге в клеточку, то написанная строчка будет длиной 250 км, потому что в тексте это число занимает 50 Мегабайт ! Такие новости, спасибо, что дочитали!
